3-4.1 Comparación Gráfica de Medias
Es muy fácil desarrollar un procedimiento gráfico para
comparar medias después de un análisis de varianza. Supóngase
que el factor de interés tiene a niveles y que y1 y2,..., ya
son los promedio de los tratamientos. Si conocemos ?, cualquier promedio
de tratamientos tendrá desviación estándar ? l n.
En consecuencia, si todas las medias de niveles de factores son idénticas,
las medias muéstrales observadas yi. se comportarán como
un conjunto de observaciones tomadas al azar de una distribución
normal con media y .. y desviación estándar ? / n.
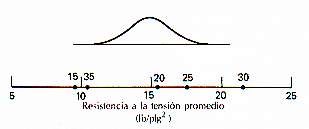
Visualicemos una distribución normal que puede deslizarse en un
eje bajo eI cual se grafican las y,, y,,..., y,. Si las medias de los tratamientos
son todas iguales, debe haber un sitio para esta distribución en
el que sea obvio que los valores y, se tomaron de la misma distribución.
Si éste no es el caso, entonces los valores de y; que parecen no
haber sido tomados de esta distribución se asocian con niveles del
factor que producen diferentes respuestas medias. El único punto
débil de este razonamiento es que se desconoce a. Sin embargo, es
posible sustituir a por ~A4S, del análisis de variancia y utilizar
una distribución t con factor de escala M5,.ln en vez de la normal.
En la Fig. 3-3 se presenta tal configuración para los datos de resistencia
del Ejemplo 3-1. Para representa tal distribución t en la Fig. 3-3,
simplemente se multiplica el valor t de la abscisa por el factor de escala
3-4.2 Contrastes
En muchos métodos de comparación múltiple se utiliza
la idea de un contraste. Considérese el problema de la prueba de
fibras sintéticas del Ejemplo 3-1. Como la hipótesis nula
H0: ?; = 0 fue rechazada, se sabe que algunos porcentajes de algodón
producen resistencia diferente a otros; sin embargo, ¿cuáles
son los que causan esta diferencia? Es posible suponer, después
de haber realizado el experimento que los porcentajes 4 y 5 producen la
misma resistencia a la tensión. Esto implica que es deseable probar
las hipótesis

3-4.3 Contrastes Ortogonales
Un caso especial del procedimiento anterior es el de contrastes ortogonales.
Dos contrastes con coeficientes (c¡) y (d;} son ortogonales si
o, en el caso de un diseño desbalanceado, si
Si se tiene a tratamientos, el conjunto de a 1 contrastes ortogonales
descomponen la suma de cuadrados Debida a los tratamientos en a 1 componentes
independientes de un solo grado de libertad. Por lo tanto, las pruebas
realizadas sobre los contrastes ortogonales son independientes, Existen
muchas maneras de elegir los coeficientes de los contrastes ortogonales
para un con- junto dada de tratamientos, Usualmente, algo de la naturaleza,
del experimento debe sugerir las comparaciones que resultan de interés,
Por ejemplo, si se tienen a = 3 tratamientos, siendo con- trol el tratamiento
l, y los tratamientos 2 y 3 los niveles reales deil factor de interés
para quien realiza el experimento, los contrastes ortogonales apropiados
podrían ser los siguientes:
Tratamientos
Coeficientes para contrastes ortogonales
I (control)
-2
0
2 (nivel l)
1
-1
3 (nivel 2)
1
1
Debe observarse que el contraste 1 con c; = 2,1,1 compara el efecto
promedio de los factores de con el control, mientras que el contraste 2
con d; = 0, 1, 1 compara los dos niveles del factor de interés.
Los coeficientes de los contrastes deben ser elegidos antes de
realizar el experimento y analizar los datos. La razón de ello es
que si las comparaciones son seleccionadas después de analizar los
datos, la mayoría de los investigadores construirían pruebas
que corresponderían a grandes diferencias observadas en los promedios,
Estas grandes diferencias pueden ser el resultado de la presencia de efectos
reales, o bien del error aleatorio. Si el investigador elige constantemente
las diferencias más grandes para hacer ]as comparaciones, el error
tipo I tiende a incrementarse. Esto es así porque en un porcentaje
excepcionalmente alto de las comparaciones seleccionadas, las diferencias
que se observan probablemente son producto del error.
Ejemplo 3-4
Consideremos los datos del Ejemplo 3-1. Existen cinco medias de tratamientos
y cuatro grados de libertad entre estos tratamientos. El conjunto de comparaciones
entre estas medias y los contrastes ortogonales asociados se presentan
a continuación:
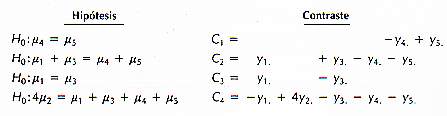
Hay que notar que los coeficientes de los contrastes son ortogonales.
Con los datos de la Tabla 3-3, se determina el valor numérico de
los contrastes y la suma de cuadrados, como se muestra en seguida:
C1 =
-1(108) + 1(54) = -54 SSc1 = (-54)2 / 5(2) = 291.60
C2 = 1(49)
+1(88)
-1(108) + 1(54) = -25 SSc2 = (-25)2 / 5(4) = 31.25
C3 =1(49)
-1(88)
= -39 SSc3 = (-39)2 / 5(2) = 152.10
C4 = 1(49) + 4(77) l(88)
l(108) I(54) = 9
SS4 =(9)2 / 5(20) = 0.81
Estas sumas de cuadrados de contrastes descomponen completamente la suma de cuadrados de tratamiento. Usualmente, las pruebas de los contrastes son incorporadas al análisis de variancia, tal como aparece en la Tab4 3-6. De esta tabla se concluye que hay diferencias significativas entre los porcentajes de algodón 4 y 5 y los de l y 3; pero que el promedio de los porcentajes l y 3 no difiere del promedio de 4 y 5, como tampoco el: 2 difiere del promedio de tos otros cuatro porcentajes.